- Profile
- Images
Location: [unknown]
Contents |
Introduction : We need more than one metaphor
This page is yet another attempt to explore and better figure if possible the structure of a space which is seriously challenging our capacities of representation, by its sheer size and complexity. We have not even agreed upon a consistent name for it. Many of us have dubbed it the "Big Tree", a reassuring metaphor, carrying in most of our cultures a familiar image of ancient wisdom and serenity. Using it, we pretty well know that we have thus ported the tree metaphor well beyond the original scope where it is relevant, the very local view of close ascendants and descendants (barring any pedigree collapse).
By no means is this global space a tree any more. From a strict mathematical viewpoint, a tree is an acyclic graph. But, as we are going to see, cycles are everywhere in this space, and just one of them would be enough to say it's not a tree.[1] At best, "Big Tree" can be kept as a symbolic, historical name. But if we want metaphors that scale, we need new ones.
In a 2009 paper[2], Mathieu Aubry writes :
The objects designated by this language are purely mathematical and abstract, but we understand them only via metaphors whose source domains motivate us to define the relation in the way we did it. Most of mathematical objects are not only understood via a single metaphor, but many. The richness of mathematical constructions comes from this wealth of metaphors, which allow us to recognize some structures from one domain in another one. Thus, via a repeated metaphorical process, mathematics creates very rich structures, and points out some of their complex properties.
The mathematical vocabulary itself is metaphoric. We name abstract concepts with terms borrowed to natural language, hoping that their original meaning helps to understand their more abstract one. Path, step, shortest path, connection, will be familiar to the city dweller, daily user of bus or train network. Elementary geometry concepts such as distance, length, diameter, circle are also portable to the more abstract graph space.
Cycle is another pervasive concept in real life. It can evoke a round trip, the return of hours and seasons. Calling cycle a closed path, coming back to its starting point, should be easily understood.
Shifting metaphors is a way to cast a different light on a reality we cannot grasp in a single view. Very often - and cycles provide one of those occasions - it will need you to jump, like Alice, down the rabbit hole. But, beware, when it comes to cycles, it's holes all the way down.
Ready to jump? Go ahead, and have fun!
Abstract
In dense endogamic clusters, cycles, aka closed paths between profiles, are pervasive patterns. Simple examples are double marriages, "short range" pedigree collapse (marriage between 1st, 2nd or 3rd cousins), but more complex examples can be found, following more or less tortuous paths involving cousins and in-laws. The Connection Finder is a convenient tool to discover such cycles, and algorithms can be implemented to discover some of them in a more systematic way.
The structure of dense endogamic clusters can be seen as a mesh of intertwined cycles rather than branches of a tree, each profile with two links or more being the crossroads of many cycles of various sizes. We claim that the global structure of most of the Big Tree - the growing set of 30+ million so-called "connected profiles" - is similar, with cycles which are simply both less frequent and larger in the areas where the WikiTree network is still sparse.
Large cycles with no internal shortcut (known as "geodesic cycles" in graph theory) can be seen as "holes" in the global mesh. They are likely to be discovered in the not yet thoroughly populated and loosely connected branches of the Big Tree. Such large holes are waiting to be mended by new shortcuts splitting them in smaller cycles, augmenting the local and global density of the network. Discovering and mending holes is a new and challenging task for Connectors. After the Outer Rim Rangers, welcome the Hole Menders!
Examples
Before introducing formal definitions, let's introduce a few examples. Cycles of all sizes are pervasive patterns in the WikiTree network, and we start by the most simple ones.
Two parents and three children
This is a simple example everybody will be familiar with. My paternal grandparents, Catherine Favennec (Favennec-1), and François-Marie Vatant (Vatant-3), had three children (Vatant-2, Vatant-6, Vatant-7). The five profiles of this family are all linked to each other by one of the relationships : parent-child, sibling, or spouse. In terms of the Connection Finder, they are at distance 1 from each other. Using the now familiar vocabulary of Circles, each one of them is in the first circle of each other. In graph theory jargon, such a pattern is called a clique. In this case, it's even a maximal clique, since there are no more children. Any other profile directly linked to one member of this family will not be directly linked to all the others (for example grandparents, uncles and aunts, spouses and grandchildren).
In the following representation, "spouse" link is blue, "parent-child" are red, and "sibling" are green.

|
In this graph representation, we can see cycles which are closed paths. Many of them can be found, the number depending if you take into account the direction of travel and/or the starting point.
- Cycles of length 5, going round the whole family, in any order, and starting from any profile. If you take direction of travel and starting point into account, there are 120 of them. If you consider that e,g,, (Vatant-3, Favennec-1, Vatant-2, Vatant-7, Vatant-6), (Vatant-6, Vatant-7, Vatant-2, Favennec-1, Vatant-3) or (Vatant-2, Vatant-7, Vatant-6, Vatant-3, Favennec-1) etc, are just different representations of the same cycle, there are only 12 cycles, each of them can be ran through 10 ways (5 possible starting points x 2 directions of travel), and represented 10 different ways.
- Cycles of length 4, each one missing one profile in the family. There again, taking direction of travel and starting point into account, 120 cycles. Otherwise, 15 cycles, each of them can be ran through 8 ways (4 possible starting points x 2 directions of travel)
- Triangles : two parents and one child (3 triangles), one parent and two children (6 triangles), and three siblings (1 triangle). Each triangle can be ran through 6 ways (3 possible starting points x 2 directions of travel)
Overall, if you take into account direction of travel and starting point, you count 300 (120+120+60) different cycles in this graph, if you don't, you count "only" 37 of them (12 + 15 + 10)
Triangles are of course the smallest possible cycles (barring an extended definition including cycles of two profiles, that we won't consider further here).
This simple example shows that, even if the concept is quite intuitive (a round trip following connections), a rigourous definition of what is a cycle, which cycles are considered identical or not, is not obvious, and there is no absolute consensus in the literature. We have not even considered here cycles passing more than one time through a given point, but only so-called "simple" cycles, of which all steps are distinct.
In the rest of the page, "cycle" will mean a simple cycle of length at least 3, not taking into account the direction of travel and the starting point.
Double marriage
Catherine and François-Marie were already in-laws when they married in 1910. Catherine's elder sister Marie-Françoise Favennec (Favennec-4) was married in 1903 with Jean-Joseph Le Vatant (Le_Vatant-1), elder brother of François-Marie. Nevermind the fact they do not share the same LNAB, civil officers in Bretagne in the late 1800s had not yet made up their mind if they should include the article in the name or not. So my cousins in Paule are "Le Vatant" until now ... anyway this double marriage, like all similar ones, creates a cycle of length 4.

|
Note an important difference with the previous example : this is not a clique any more, there is no direct relationship between the in-laws. In other words, this cycle cannot be split in smaller ones (triangles). Such a cycle is called in graph theory a geodesic cycle. See the Graph theory vocabulary section for a more precise mathematical definition.
Pedigree collapse
Pedigree collapse can be defined by the marriage between cousins more or less removed. Every instance of pedigree collapse creates a cycle. Marriage of first cousins creates a circle of length 4, second cousins a circle of length 6, etc. Marriage of cousins once removed creates a cycle of odd length.
Catherine and François-Marie were not only in-laws when they married, they were also third cousins once removed! Their marriage creates a cycle of length 9.

|
As the previous one, this cycle is geodesic and almost certainly bound to stay so, even if it's less obvious than in the previous case. The explanation is that all profiles in this cluster have been thoroughly searched and completed, and no further shortcut seems likely to be found in the future. This is a "hole beyond repair", so to speak. But it's a small hole, its diameter (maximal distance between two profiles) is only 4. We'll see later on that much larger holes can be found!
Mesh of cycles in endogamic clusters
In endogamic clusters, many profiles are the crossroads of many intertwined cycles. The following example shows some cycles around Pierre-Marie Vatant (an uncle of the above François-Marie and Jean-Joseph) and his four spouses.

|
This is a very partial representation, including more cycles would make a planar representation quite challenging if possible at all, but it provides a glimpse of the local structure of WikiTree network in dense endogamic areas.
The Life Cycle of Cycles
Cycles can be created basically two ways, bottom-up or top-down.
Bottom-up : Cycles are likely to be created if you systematically explore and complete your first circles, in order to grow your CC7 (or the one of your favourite profile), and in particular if the population of those circles is as endogamic as the one presented above. Such cycles will mostly be of small size (typical length in the 5 to 15 range). Larger ones can appear if you are lucky enough to see your close circles meet some far-flung branch of the Big Tree. But in such a case, you are switching to the top-down scenario.
"Top-down" : The scenario illustrated below appears as the most likely to create larger cycles, with length typically in the 20 to 50 range. It relies on a common process, the connection to the Big Tree of a previously so-called "unconnected branch".
Step 1 : Primary connection to the Big Tree
When a new branch is connected to the Big Tree, the first connection path includes a bottleneck profile, or even several of those. Connecting a branch to another one which is already spreading far from the center can result in tortuous branches extending as far as the Outer Rim of the Tree.
The single connection point, here the marraige of Peter and Jeanne, is a "single point of failure" in the connection. If this link is cut, the branch of Jeanne at left is no more connected.

|
Step 2 : A secondary connection creates a cycle
In the following example, a secondary connection comes from the discovery that P1 and P10 were siblings. Before this new connection, the distance from P1 to P10 was 9, after the connection, they are at distance 1.

|
The new cycle, barring further changes, is geodesic, providing (P1, P2, ..., P10) was a shortest path before the secondary connection. A secondary connection always creates a geodesic cycle : just before the connection, there always existed a shorter path between the secondary connection points (here, P1 and P10)
Unfortunately, as soon as this secondary connection is effective, the Connection Finder "forgets" where the cycle has been closed. And if the secondary connection brings the tip of the formerly unconnected branch closer to the center, even if it was before a long branch extending outwards to the Outer Rim, it's now pulled back inwards, under the radars of the Outer Rim Rangers.
Step 3 : Mending the holes
A hole created at Step 2 is likely to be further split in smaller cycles, until no further shortcut can be found. Providing someone works on it.
But it might also stay put at Step 2. Not showy enough to be detected in the Outer Rim, but peripheral enough to be forgotten by the central activity. An algorithm able to detect those large and mostly invisible holes, would be precious. How can we mend the holes if we can't find them?
Another difficult question is : when can we say a hole is "beyond repair", in other words small enough that we can be sure no more shortcut will be found? This question is discussed in a further section.
Finding cycles with the Connection Finder
The Connection Finder application allows you to strike off a profile (or more) from the shortest path to find alternative ones (generally longer, but not always). If two alternative paths go through completely different profiles (which is often the case), putting them together provides for a cycle.
Simple (but not geodesic) example
The shortest path from Maurice Vatant to his granddaughter Marie-Françoise Vatant goes of course through Jean-Joseph Vatant , son of Maurice and father of Marie-Françoise.

|
Striking Jean-Joseph from the path yields an alternative path of length 5.

|
This alternative path is quite short, once again thanks to local endogamy. Not really a case of genuine pedigree collapse, but close : two cousins, grandchildren of Maurice, have married two siblings Le Bescond. Reintroducing Jean-Joseph in the picture, we get a cycle of length 7.

|
Is this cycle geodesic? No, because there is a shortcut between Jean-Joseph and his sister Jeanne! But we have a smaller one of size 6, if we remove their father Maurice. A nice particular pattern : two siblings and their two children who married two other siblings. A mixture of pedigree collapse and double marriage. That one is geodesic and not reducible to smaller cycles. Try to find a similar one in your circles!
Two geodesic even cycles
Using the same method as in the previous example, the shortest path from my paternal grandfather to my mother is a 2 steps path going through my father (Vatant-2).
Striking Vatant-2 from the path, the Connection Finder finds a shortest path of length 20. Adding back Vatant-2 yields a cycle of length 22. To check that this cycle is geodesic, we just have to make sure there is no shortcut between Vatant-2 and his antipode profile Boucher-3785. The Connection Finder confirms those two profiles are at distance 11. Since the cycle is even, there are two alternatives paths from Vatant-2 to Boucher-3785, passing through the two opposite halves of the cycle, and both of length 11.

|
Note : the private profiles between Le-Bozec-5 and Galliou-2 cannot be checked in public views. In this case they are in the first circles of a cousin whom I fully trust, so I'm quite confident this path is OK. But private profiles in paths and cycles are generally speaking making things more complex.
Another similar example, provided by Eva Ekeblad, is based on two alternative paths from her grandfather Gustaf Persson to Christina Eriksdotter (first path and alternative path), both of length 9. Put together they form a geodesic cycle of length 18.

|
A odd "almost geodesic" cycle
The following example, shows that in general, you have indeed to check *all* pairs of antipodes before declaring a cycle is geodesic.
Starting from the reference profile Queen Elizabeth II (Windsor-1), we have used the Connection Finder to find a shortest path to a random profile Moy-237. This path is of length 17 (first half of the first column in the following table).
Striking the second profile in the path (Windsor-24), the Connection Finder finds an alternative path which is one step longer, and goes through completely different profiles.
Using those two paths back and forth, we get a cycle of 35 profiles starting from Windsor-1. Its is a odd cycle, so we have to check the distances for 35 pairs of antipodes. For the cycle to be geodesic, all those distances should be equal to 17 (35 = 2x17 + 1) in the global graph. The results are gathered in the following table (data as of December 27, 2023).
| Profile | Antipode | distance |
|---|---|---|
| Windsor-1 | Moy-237 | 17 |
| Windsor-24 | Bantick-4 | 17 |
| Armstrong-Jones-1 | Bantick-2 | 17 |
| Armstrong-Jones-9 | Bantick-16 | 17 |
| Coombe-669 | Bantick-24 | 17 |
| Coombe-668 | Bantick-51 | 17 |
| Beddome-25 | Noble-5477 | 17 |
| Beddome-17 | Noble-8047 | 17 |
| Beddome-53 | Nobel-217 | 17 |
| Beddome-37 | Andreasson-526 | 17 |
| Beddome-34 | Carlsson-2181 | 17 |
| Beddome-26 | Johnsson-412 | 17 |
| Dossetor-23 | Wijkmark-174 | 17 |
| Dossetor-5 | Bernadotte-35 | 16 |
| Green-21351 | Bernadotte-9 | 15 |
| Green-21409 | Battenberg-62 | 17 |
| Green-26236 | Battenberg-12 | 17 |
| Moy-237 | Schleswig-Holstein-Sonderburg-Glücksburg-1 | 17 |
| Bantick-4 | Windsor-1 | 17 |
| Bantick-2 | Windsor-24 | 17 |
| Bantick-16 | Armstrong-Jones-1 | 17 |
| Bantick-24 | Armstrong-Jones-9 | 17 |
| Bantick-51 | Coombe-669 | 17 |
| Noble-5477 | Coombe-668 | 17 |
| Noble-8047 | Beddome-25 | 17 |
| Nobel-217 | Beddome-17 | 17 |
| Andreasson-526 | Beddome-53 | 17 |
| Carlsson-2181 | Beddome-37 | 17 |
| Johnsson-412 | Beddome-34 | 17 |
| Wijkmark-174 | Beddome-26 | 17 |
| Bernadotte-35 | Dossetor-23 | 17 |
| Bernadotte-9 | Dossetor-5 | 15 |
| Battenberg-62 | Green-21351 | 16 |
| Battenberg-12 | Green-21409 | 17 |
| Schleswig-Holstein-Sonderburg-Glücksburg-1 | Green-26236 | 17 |
We find that 31 out of 35 pairs of antipodes are indeed at distance 17, but 4 of them are at distance 15 or 16, with a shortest path passing through profiles out of the current cycle. For example the shortest path from Dossetor-5 to Bernadotte-35. We could use this shortcut to define a new and smaller cycle, and check if that one is geodesic ...
Finding cycles with WikiTree+
Following the first exchanges on G2G around previous examples, Aleš has developed a function on WikiTree+, leveraging the Connection Finder, based on the above method of "striking a profile in the path". This section is an introduction to the function, and how to interpret its output.
The PathCycle function
The URI of the function is : https://plus.wikitree.com/default.htm?report=disp3
The function takes as input two profiles ID1 and ID2, which must respect two conditions
- The path from ID1 to ID2 must contain at least 3 profiles (in other words distance of ID1 to ID2 is at least 2).
- ID1 and ID2 privacy level must be Open, Public, or Private with Public Family Tree, in order to be present in WikiTree+.
Calling the Connection Finder, the function first computes a shortest path from ID1 to ID2. Then it will process all the triples (a,b,c) of successive profiles in this path. If the length of the path is n, the number of such triples is n-1.
For each triple, it calls the Connection Finder again to find the shortest path from a to c excluding b. Adding back b to this path to build a cycle. Using the Connection Finder again, it checks if this cycle is geodesic or not, by computing antipodal distances.
For each triple, the results are displayed in two tables. The first table is the triple (a,b,c) itself, with details of each profile. The second table contains a cycle starting with b (first line, profile 0) then all profiles of the shortest path from a to c excluding b.
The length of the cycle is displayed. For each profile of the cycle, the antipodal distance(s) is/are displayed. There is one value if the cycle is even, two values if the cycle is odd.
Details for each profile in the cycle are taken from the weekly WikiTree+ dump, but distances and paths are computed from the real time data of the Connection Finder. If the data retrieved by the Connection Finder contains profile IDs not (yet) present in the WikiTree+ dump (because they are private, or created after the current dump), they will be marked as "private/unlisted".
The function is resource consuming, don't submit a too long path to avoid timeout, (or split in smaller paths you will submit separately). The process can be long, the timeout is fixed at 10s, but partial results are cached, so you can relaunch the query several times, more results will be found each time, until you get the whole of them.
To get familiar with the function, start with a simple path of length 3, e.g., ID1 = your mother and ID2 = your paternal grandfather (assuming your parents are linked by a "spouse" relationship).
You will get something similar to the following, retrieving the cycle of length 22 detailed in previous section.
https://plus.wikitree.com/default.htm?report=disp3&WikiTreeID1=Vatant-3&WikiTreeID2=Corre-22
As for any WikiTree+ function, you have to click the blue "Find cycles" button.
Interpreting the output
This section provides clues for the most frequent outputs. You may stumble on cornercases which you are welcome to post in the dedicated G2 conversation.
No alternate connection
This message is displayed above the triple (a,b,c) table when the only path from a to c is the one passing through b. The profile b is a "point of failure" or "bottleneck" (in graph theory jargon, an "articulation node") in the network. If you remove this profile, the graph is disconnected. Generally, it means that either a or c belong to a branch connected to the Big Tree uniquely by profile b. This can be obvious if the said branch is quite small, but if it's bigger, this result can be interesting. Of course, in this case, no cycle is found!
Geodesic cycle
This is not the most frequent output, as will be explained in the further section, but will happen in about 30% of cases (on the basis of samples tested). In such a case, you have discovered a "hole" in the network. It is the minimal cycle (minimal length) containing the triple which has been processed. It's up to you to figure if and how it can be mended. See further sections.
Not (but almost) geodesic cycle
This seems to be the most frequent output (on the basis of samples tested). The cycle is not geodesic, but antipodal distances are either equal to the expected value (half the length of the cycle) or this value minus 1. For example, for a cycle of length 22 or 23, the antipodal distances will be either 11 or 10. This generally means the following situation :
Let (a,b,c) be the triple processed. The shortest path from a to c is going through b. The shortest path from c to a not going through b is of the form (c,d, ...., z,a). The cycle obtained by putting back b between a and c, can be represented in the form (.... ,z,a,b,c,d, ...). What often happens is that the distance from b to d, or from z to b, is 1. For example b and d are siblings, c is a common parent. Or z and b are spouses, and a is their child. One can easily figure that among all the choices of a and c in the first circle of b, this will happen more often than the opposite situation (z to b and b to d both equal to 2). With such a shortcut, of course the cycle is not geodesic, but almost. You only need to "bypass" one profile.
It's easy to figure which one has to be bypassed. If for example the distance from b to d is one, you have to bypass c to get a geodesic cycle. To view the new geodesic cycle with the PathCycle function, restart it with ID1=a and ID2=d (instead of c).
Note : this should be more understandable with images (to be delivered)
Length of the cycle(s)
In interpreting the length of the cycles found by the function, one you avoid jumping to conclusions, the following should be taken as generally observed patterns, which certainly suffer many exceptions.
- Short cycles (length below 10) are typically found in endogamic communities, they indicate things like short-range pedigree collapse, double marriage, marriage between in-laws, or more sophisticated patterns. It wil often be necessary to take a pencil and a sheet of paper to figure them out!
- Average cycles have typical length in the 15 to 25 range. They will appear in the dense, but not particularly endogamic parts of the Tree.
- Long cycles have length in the 30 to 50 range. They will appear around profiles with a few long connections to the bulk of WikiTree.
Example

|
The above picture is a summary of the cycles found by the PathCycle function with input ID1=Segalen-10 and ID2=De_Rothschild-9 (data as of 17 Jan 2024)
The shortest path between those two profiles is of length 13, the function will process 12 triples.
The seven first triples belong to the same cycle, of length 37. On the picture, six profiles between Segalen-10 and Drach-68 have been skipped, they all belong to this rather long cycle. As mentioned in the above section, this means Segalen-10 is sparsely connected. He has only a line of connection through his father Segalen-9, and another one through his son Segalen-18. He has a quite low CC7 (108, as of 17 Jan 2024), another indication of the sparsity of the graph around him.
At the opposite, the cycles found at the end of the path are short. The last one, of length 5, indicates a marriage between first cousins. The Rothschild family is notoriously endogamic!
Minimal cycles (are geodesic)
Shawn's algorithm
Shawn Ligocki has developed an algorithm finding the cycles of minimal length (aka minimal cycles) containing a given profile. Minimal cycles are geodesic (this is quite easy to prove), but not the other way round. Finding minimal cycles will not yield all geodesic cycles (we've seen this target is unreachable), but hopefully an important subset of them.
Shawn's program runs on the Bipartite Network he had introduced in his Jan 2021 publication : https://www.sligocki.com/2021/06/24/wikitree-network-definition.html. The main advantage of using the Bipartite Network is to avoid the noise of all the small cycles present in the family cliques, as explained in the first example of the introduction. The minimal cycles found that way should be of length 4 or more.
This algorithm was expected to discover large geodesic cycles in the sparsely connected and populated suburbs of the Big Tree, midway between the dense core and the Outer Rim. Typically, those large would be stuck at Step 2 of the above described life cycle of cycles.
First run of the program yielded some surprises ...
First results
Data updated : 27 Apr 2024.
The longest minimal cycles found by Shawn's program in Jan 2024 are gathered in the following table. 24 cycles of length over 50 have been found. They can be checked by using the PathCycle function for the provided values ID1 and ID2. In each case, those profiles are at distance 2 of each other, the PathCycle will process only one triple, and the cycle should be found geodesic. The last column gives the updated length as of 27 Apr 2024, some holes have been drastically reduced in size.
| Jan 24 | ID1 | ID2 | Apr 24 |
|---|---|---|---|
| 95 | Chandler-9431 | Defountain-1 | 47 |
| 82 | Van_der_Mersch-964 | Van_der_Mersch-856 | ? Van_der_Mersch-964 not found |
| 75 | Morais_Barros-1 | Moraes_Barros-4 | 75 |
| 70 | Mieg_Eislin-2 | Mieg-273 | 64 |
| 70 | Mamikonian-11 | Mamikonian-22 | 70 |
| 68 | Bushrod-133 | Bushrod-131 | 8 |
| 64 | Hartman-478 | Deventer-1 | 64 |
| 64 | Essers-64 | Essers-52 | 64 |
| 63 | Grassart-44 | Grassart-14 | 63 |
| 62 | Jørgensen-4732 | Busk-2 | 62 |
| 62 | McAteer-16 | Poole-6989 | 57 |
| 62 | Bark-101 | Woudt-2 | 63 |
| 61 | Strudwick-114 | Strudwick-115 | 38 (not geodesic) |
| 60 | Swierc-5 | Wiatrek-2 | 60 |
| 59 | Hönig-63 | Kurtz-1009 | 59 |
| 59 | Lenz-780 | Nelson-19379 | 59 |
| 58 | Lourdelle-8 | Lourdelle-1 | 58 |
| 57 | Štípek-14 | Votava-14 | 57 |
| 57 | Bas_Isaak-4 | Wormser-30 | 56 |
| 56 | Nesje-8 | Hansen-18214 | 45 |
| 54 | Goodrich-8568 | Hayworth-328 | 21 |
| 54 | Motshagen-5 | Hampe-46 | 44 |
| 52 | Kusters-11 | Van_Gerwen-70 | 51 |
| 51 | De_Maesschalck-29 | Pieters-2203 | 51 |
The first case was a real outlier, similar to the Hamdani branch in the Outer Rim (with similar ancestors). Nevertheless, its structure is consistent with the expected life cycle scenario we have described above : secondary connection of large far-flung branches, and a hole stuck at Step 2, because it goes through space-time regions of WikiTree poorly known and with basically no task force to improve them.
Other examples do not look like they result from the scenario described in the "Life Cycle of Cycles" section. They do not contain "exotic" branches, the profiles are mostly European or North-American Anglo-Saxons, they don't extend very far either in the past or towards the Outer Rim regions. Moreover, they are passing through a lot of different branches.
Even if such cases are not many, they indicate that relatively large holes can hide even in dense parts of the graph. It is of course challenging to see if, when and how such holes will be mended.
Open Issues
How large are the largest holes ?
An absolute upper bound of the size of a hole is given by the diameter of the Big Tree itself. The follow-up of distant profiles in the Outer Rim study has shown that over the last three years, the diameter of the Big Tree has hovered around 150. But the Outer Rim profiles are generally the tip of far-flung branches, connected to the bulk of the Tree by tortuous paths and bottlenecks, so it's very unlikely to find geodesic cycles passing through such profiles.
The upper bound for the diameter of geodesic cycles is certainly much less than the 150 limit. So far, the various approaches have not yielded cycles of length over 100, and length over 50 seems very unfrequent. A length of 100 would mean a diameter of 50, one third of the Big Tree current diameter.
When is a hole deemed "beyond repair"?
Let's take the example of the cycle of length 22 presented above (passing through Vatant-2). All its antipodal distances are equal to 11. This cycle could be said "beyond repair" if we could confidently assume that no shortcut of length 10 or less will ever be found between any of the 11 antipodes pairs. Such a conclusion would be a bold one in the currrent state of affairs. It would mean that for all profiles in the cycle, the 5 first circles (aka CC5) would have been completed, and no overlapping of those circles for antipodes pairs has been found.
This is obviously not the case in the current state of affairs, and it would take a lot of work ... and time, to achieve. Two (private) profiles in the cycle are living, born in the 1970s, and they have children. To deem their 5 circles complete, we have to wait for 5 generations of their descendants, and their (potentially endogamic) marriage(s). This brings us, at 30 years by generation, to people born by 2120, married by 2150 ... Supposing this cycle is still geodesic by then, a shortcut could happen over one century from now.
The other way round, in the past, the two oldest profiles in the cycle were born by 1760. Their 5th circle in the direction of ancestors brings us to 1600 or before, next to or beyond the documentary horizon.
Only much smaller geodesic cycles can be deemed beyond repair. A cycle of length 8, with antipodal distance of 4, will only need to complete the CC2 of all its profiles. This can be challenging, but not completely unrealistic to achieve, bearing in mind that to deem a profile "complete" is often a bold assumption of our knowldge's completeness.
Looking at larger holes, figures yielded year after year by the 100 Circles project tend to show that in the long run, almost all profiles in the Big Tree could be at distances as low as 20 from each other, the mean distance being currently around 25. We can safely conjecture that geodesic cycles of diameter above 25 (that is, length 50 or more) are very likely mendable.
Size of cycles and CC7
As the Segalen - Rothschild example illustrates, the size of cycles containing a profile is not independent of the density of the graph around this profile, which is otherwise measured by the population of close circles (aka CC7). One can expect to find small cycles around profiles with a high CC7, the more so if those profiles belongs to some endogamic community with large families, and to find large cycles rather in the sparsely populated areas of the Big Tree. But preliminary examples found by Shawn's program show that things are maybe not that simple. Large geodesic cycles can also pass through dense parts of the network. More work is needed on this topic, and more data gathered.
Graph theory vocabulary
Geodesic paths and geodesic cycles
If you are familiar with the Connection Finder (you should be), you know what is a "shortest path" between two profiles. In graph theory, such a path is called a "geodesic" path. We have already used this term for cycles in the examples. So what is the definition of a geodesic path?
A path between two profiles is called geodesic if its length is minimal.
This definition needs a bit of attention to the details.
- "Minimal length" means the smallest value of the length, among all possible paths linking the two profiles. If they are both thoroughly connected, there is often more than one shortest path. The shortest path given in WikiTree by the Connection Finder is a geodesic one, but it's good to bear in mind that it is the first one provided by a complex algorithm. The Connection Finder does not indicate if there are alternative shortest paths, and if yes, how many of them.
- A path defined as a subset of consecutive profiles in a geodesic path is also geodesic. For example if (p1, p2, p3, p4, p5, p6, p7, p8) is geodesic, so is e.g., (p2, p3, p4, p5). Otherwise said, a shortest path between two profiles in a geodesic path P is also a part of P. No possible shortcut between p2 and p5.
A cycle is said "geodesic" if a shortest path between two profiles of the cycle is part of the cycle.
In other words, in a geodesic cycle, there is no "shortcut" between two profiles. A geodesic cycle, past a certain size (not clearly defined), can be dubbed a "hole", because in a planar representation of the cycle, there is no path "inside" it. We have seen examples in the previous section.
In the intricated example of the mesh of Vatant-6, it's easy to find several cycles which obviously include smaller ones, hence are not geodesic. But since the representation is very partial, maybe some of the smaller cycles which look geodesic in this view will be no more when other profiles in the local cluster are added.
Finding geodesic cycles, and figuring if they are bound to stay that way forever or likely to be split in smaller circles, are both difficult tasks.
Antipodes
A pair of profiles of which distance is maximal in a cycle are called antipodes. Those are important because they will be used to check is a cycle is geodesic or not.
In this definition, "maximal distance" is defined relatively to the cycle (ignoring the rest of the graph). If the cycle is not geodesic, shortcuts entail that distances in the global graph might be shorter. See examples further on.
The pattern and the number of antipodes pairs depends on the parity of the cycle's length.
Even cycle
An even cycle is a cycle with an even length (n=2k).
An even cycle has k pairs of antipodes, and each profle has exactly one antipode.
Example : Cycle of length 12, with 6 pairs of antipodes.

|
Odd cycle
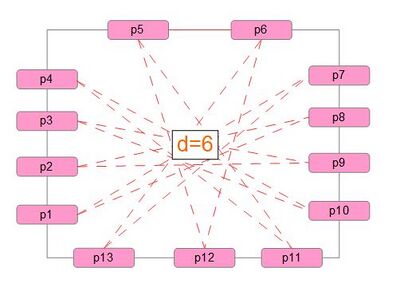
A odd cycle is a cycle with a odd length (n=2k+1).
A odd cycle has n pairs of antipodes, each profle has exactly two antipodes.
Example : Cycle of length 13, with 13 pairs of antipodes.
|
References
- ↑ Wikipedia https://en.wikipedia.org/wiki/Tree_(graph_theory) Tree (graph theory)
- ↑ Aubry, Mathieu, Metaphors in Mathematics: Introduction and the Case of Algebraic Geometry (September 26, 2009). Available at SSRN: https://ssrn.com/abstract=1478871 or http://dx.doi.org/10.2139/ssrn.1478871
- Have you checked the WikiTree+ function to find cycles? Jan 11, 2024.
- Cycles and Holes in the Big Tree Jan 5, 2024.
- Login to request to the join the Trusted List so that you can edit and add images.
- Private Messages: Contact the Profile Managers privately: Eva Ekeblad, Shawn Ligocki, and Bernard Vatant. (Best when privacy is an issue.)
- Public Comments: Login to post. (Best for messages specifically directed to those editing this profile. Limit 20 per day.)
- Public Q&A: These will appear above and in the Genealogist-to-Genealogist (G2G) Forum. (Best for anything directed to the wider genealogy community.)